Šī raksta tēma ir polikarbonāta nojumes aprēķins ar savām rokām. Mums jāiemācās aprēķināt galvenos konstrukcijas parametrus, kas saistīti ar tās izturību un izmēriem. Tātad, ejam.

Ko mēs aprēķinām
Mums jāiemācās aprēķināt:
- Polikarbonāta biezums un kastes slīpums atkarībā no paredzamās sniega slodzes uz kvadrātmetru.
- Arkas vāka izmēri (kas ģeometrijas ziņā nozīmē loka garuma aprēķināšanu).
Precizitātei: mēs pētām veidus, kā aprēķināt loku zināmam sektora rādiusam un leņķim, kā arī gadījumam, kad zinām tikai attālumus starp arkas virsmas galējiem punktiem.
- Minimālais caurules posms ar zināmu lieces slodzi.
Šādā secībā mēs turpināsim.
Lakojuma un pārklājuma biezums
Sāksim ar sniega slodzes aprēķinu.
Pirms mēs izdomājam, kā aprēķināt polikarbonāta nojume, mēs formulēsim pāris pieņēmumus, uz kuriem balstās aprēķins.
- Dotie dati attiecas uz augstas kvalitātes materiālu bez ultravioletā starojuma iznīcināšanas pazīmēm. Polikarbonāts bez UV filtra kļūst trausls pēc 2-3 gadu darbības gaismā.

- Mēs apzināti ignorējam kastes ierobežoto deformācijas stabilitāti, uzskatot to par absolūti spēcīgu.
Un tagad - tabula, kas palīdzēs izvēlēties optimālo polikarbonāta biezumu un kastes piķi.
| Slodze, kg/m2 | Kastes šūnu izmēri ar polikarbonāta biezumu, mm | |||
| 6 | 8 | 10 | 16 | |
| 100 | 1050 x 790 | 1200x900 | 1320x920 | 1250x950 |
| 900x900 | 950x950 | 1000x1000 | 1100x1100 | |
| 820x1030 | 900x1100 | 900x1150 | 950x1200 | |
| 160 | 880x660 | 1000x750 | 1050 x 750 | 1150x900 |
| 760x760 | 830x830 | 830x830 | 970x970 | |
| 700x860 | 750x900 | 750x950 | 850x1050 | |
| 200 | 800x600 | 850x650 | 950x700 | 1100x850 |
| 690x690 | 760x760 | 780x780 | 880x880 | |
| 620x780 | 650x850 | 700x850 | 750x950 | |
Arch
Aprēķins pēc rādiusa un sektora
Kā aprēķināt nojumes arku, ja zinām lieces rādiusu un loka sektoru?

Formula izskatīsies šādi: P=pi*r*n/180, kur:
- P ir loka garums (mūsu gadījumā polikarbonāta loksnes vai profila caurules garums, kas kļūs par rāmja elementu).
- pi ir skaitlis "pi" (aprēķinos, kuriem nav nepieciešama ārkārtīgi augsta precizitāte, parasti tiek pieņemts vienāds ar 3,14).
- r ir loka rādiuss.
- n ir loka leņķis grādos.
Kā piemēru ar savām rokām aprēķināsim nojumes arkas garumu ar rādiusu 2 metri un sektoru 35 grādi.
P \u003d 3,14 * 2 * 35 / 180 \u003d 1,22 metri.
Darba procesā bieži rodas pretēja situācija: nepieciešams pielāgot loka rādiusu un sektoru noteiktam arkas garumam. Iemesli ir skaidri: polikarbonāta cena ir pietiekami augsta, lai samazinātu atkritumu daudzumu.
Acīmredzot šajā gadījumā sektora un rādiusa reizinājums būs vienāds ar P/pi*180.
Mēģināsim ievietot arku zem standarta loksnes 6 metru garumā. 6/3,14*180=343,9 (ar noapaļošanu). Tālāk - vienkārša vērtību atlase ar kalkulatoru rokā: piemēram, loka sektoram 180 grādi var ņemt rādiusu, kas vienāds ar 343,9 / 180 \u003d 1,91 metriem; ar 2 metru rādiusu sektors būs vienāds ar 343,9 / 2 \u003d 171,95 grādiem.
Aprēķins pēc akordiem
Kā izskatās polikarbonāta nojumes ar arku konstrukcijas aprēķins, ja mums ir informācija tikai par attālumu starp arkas malām un tās augstumu?
Šajā gadījumā tiek piemērota tā sauktā Huygens formula. Lai to izmantotu, domās sadalīsim arkas galus savienojošo akordu uz pusēm, pēc tam novelkam perpendikulu akordam vidū.
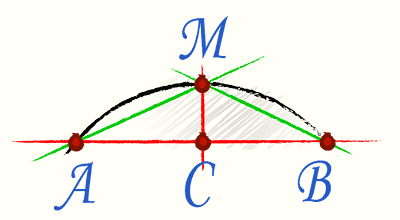
Pašai formulai ir forma Р=2l+1/3*(2l-L), kur l ir AM horda un L ir AB horda.
Svarīgi: aprēķins dod aptuvenu rezultātu. Maksimālā kļūda ir 0,5%; jo mazāks ir arkas leņķiskais sektors, jo mazāka ir kļūda.
Aprēķināsim arkas garumu gadījumam, kad AB \u003d 2 m un AM - 1,2 m.
P=2*1,2+1/3*(2*1,2-2)=2,4+1/3*0,4=2,533 metri.
Sekcijas aprēķins ar zināmu lieces slodzi
Diezgan dzīves situācija: daļa no nojumes ir zināma garuma vizieris. Mēs varam aptuveni novērtēt maksimālo sniega slodzi uz to. Kā izvēlēties šādas sekcijas profila cauruli sijām, lai tā zem slodzes nelocītu?

Piezīme! Mēs apzināti nepieskaramies tam, kā aprēķināt nojumes slodzi. Sniega un vēja slodzes novērtējums ir pilnīgi pašpietiekama tēma atsevišķam rakstam.
Lai aprēķinātu, mums ir vajadzīgas divas formulas:
- M = FL, kur M ir lieces moments, F ir spēks, kas tiek pielikts sviras galam kilogramos (mūsu gadījumā sniega svars uz viziera), un L ir sviras garums (garums sijas, kas iztur sniega slodzi, no malas līdz punktam) centimetros.
- M/W=R, kur W ir pretestības moments un R ir materiāla izturība.
Un kā šī nezināmo vērtību kaudze mums palīdzēs?
Pats par sevi nekas. Aprēķiniem trūkst dažu atsauces datu.
| tērauda marka | Stiprums (R), kgf/cm2 |
| St3 | 2100 |
| St4 | 2100 |
| St5 | 2300 |
| 14G2 | 2900 |
| 15GS | 2900 |
| 10G2S | 2900 |
| 10G2SD | 2900 |
| 15HSND | 2900 |
| 10HSND | 3400 |
Atsauce: Profesionālām caurulēm parasti izmanto St3, St4 un St5 tēraudus.
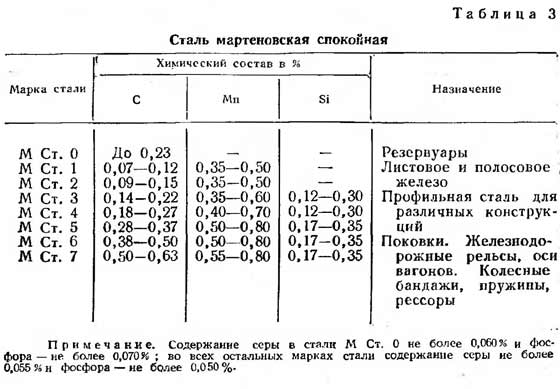
Tagad, pamatojoties uz mūsu rīcībā esošajiem datiem, mēs varam aprēķināt profila caurules lieces pretestības momentu. Darām to.
Pieņemsim, ka uz divu metru nojumes ar trim nesošajām sijām, kas izgatavotas no St3 tērauda, sakrājas 400 kilogrami sniega.Lai vienkāršotu aprēķinus, mēs piekritīsim, ka visa slodze krīt uz viziera malas. Acīmredzot katra sija slodze būs 400/3=133,3 kg; ar divu metru sviru lieces moments būs vienāds ar 133,3 * 200 \u003d 26660 kgf * cm.
Tagad mēs aprēķinām pretestības momentu W. No vienādojuma 26660 kgf * cm / W = 2100 kgf / cm2 (tērauda izturība) izriet, ka pretestības momentam jābūt vismaz 26660 kgf * cm / 2100 kgf / cm2 = 12,7 cm3.
Kā pretestības momenta vērtība mūs novedīs pie caurules izmēriem? Izmantojot GOST 8639-82 un GOST 8645-68 ietvertās sortimenta tabulas, kas regulē kvadrātveida un formas cauruļu izmērus. Katram izmēram tie norāda atbilstošo pretestības momentu, bet taisnstūra sekcijai - pa katru no asīm.
Pēc tabulu pārbaudes mēs noskaidrojam, ka kvadrātveida caurules minimālais izmērs ar nepieciešamajiem raksturlielumiem ir 50x50x7,0 mm; taisnstūrveida (ar lielākās malas vertikālo orientāciju) - 70x30x5,0 mm.

Secinājums
Ceram, ka neesam pārpūlējuši lasītāju ar sausu figūru un formulu pārpilnību. Kā vienmēr, papildu informāciju par polikarbonāta nojumju aprēķināšanas un projektēšanas metodēm var atrast šī raksta videoklipā. Veiksmi!
Vai raksts jums palīdzēja?